
Четные и нечетные числа для дошкольников
Ваш ребенок уже знает, что такое цифры, легко считает до двадцати? Познакомьте его с четными и нечетными числами. Как это сделать? Вы найдете ответ в нашей статье.
Как объяснить дошкольнику, что такое четные и нечетные числа?
Итак, четное число — это целое число, которое можно поделить на два без остатка. Нечетное, соответственно, поделить без остатка нельзя. Объяснить это лучше на «съедобных» примерах:
“Смотри: у нас с тобой три яблока. Как нам их поделить на двоих поровну?»
Скорее всего дошкольник придёт к выводу, что разделить без остатка эти яблоки невозможно, придется кому-то предложить третье яблоко или разрезать его пополам.
Потом предложите разделить четыре яблока. Обратите внимание ребенка, что в этом случае вам достанется поровну по два яблока и делиться с кем-то не возникнет необходимости.
Подскажите ребенку, что четные и нечетные числа чередуются и их легко запомнить: если 1 — нечетное число, следом за ним идет 2 — четное, 3 — нечетное и так далее.
Покажите ребенку любое двух- или трехзначное число и предложите определить, четное оно или нечетное. Попросите ребенка прокомментировать свой ответ. Поделитесь секретом: определять, четное число или нечетное, нужно по последней цифре. Следовательно числа, оканчивающиеся на 0, 2, 4, 6, 8 — четные, а на 1, 3, 5, 7, 9 — нечетные.
Получение четных и нечетных чисел при выполнении арифметических действий
Не нужно вкладывать в голову ребенка уже готовые знания. Эффективнее, когда он получает и перерабатывает информацию, столкнувшись с ней на практике.
Попросите ребенка на конфетах посчитать и определить, какое число — четное или нечетное — получится, если сложить два четных числа.
Выполнив примеры, приходим к следующим закономерностям, которые касаются как вычитания, так и сложения:
- чётное ± чётное = чётное (2 +4 = 6);
- чётное ± нечётное = нечётное (8 — 5 = 3);
- нечетное ± нечетное = четное (3 + 7 = 10).
При умножении будут следующие результаты:
- четное * четное = четное (8 * 2 = 16);
- четное * нечетное = четное (4 * 3 = 12);
- нечетное * нечетное = нечетное (3 * 5 = 15).
Закономерности деления четных и нечетных чисел:
- чётное : чётное — результат может быть как чётным, так и нечётным (12 : 4 = 3; 16 : 4 = 4);
- чётное : нечётное = чётное (18 : 3 = 6);
- нечётное : чётное — результат не может быть целым числом, поэтому нельзя говорить о его четности или нечетности;
- нечётное : нечётное = нечётное (27 : 9 = 3).
Упражнения с четными и нечетными числами
Любое полученное знание требует закрепления, иначе оно быстро выветривается из памяти.
Для закрепления навыка определения четных и нечетных чисел хорошо подойдут следующие упражнения:
1. Взрослый называет числа. Задача ребенка — определить, четное это число или нечетное.
2. Игра с мячом. Взрослый оговаривает правила игры: он кидает мяч и говорит число. Задача ребенка — поймать мяч, если взрослый называет четное число, и отбить его — если нечетное.
3. Вам понадобятся макеты домов и дороги, а также карточки с числами от 1 до 20. Сообщите ребенку, что в домах с одной стороны от дороги живут четные числа, а с другой — нечетные. Ребенку нужно расселить числа по домам.
4. Тренируйте навык определения четности числа при любом удобном случае. Например, на прогулке выясняйте четный ли номер у машины, дома. Обычно эти знания даются дошкольнику легко и в будущем помогают в учебе в школе.
5. Выполнение письменных упражнений. Предлагаем вам несколько таких заданий.
Задание 1
Почитай сумму чисел и определи, какое число получилось — четное или нечетное.
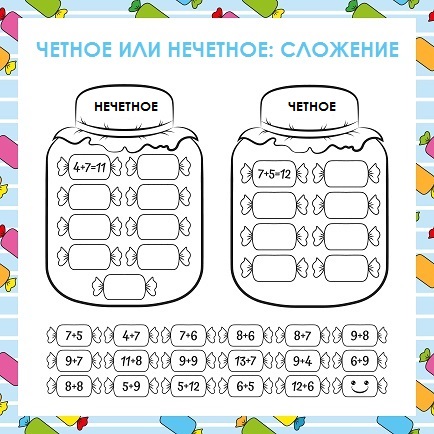
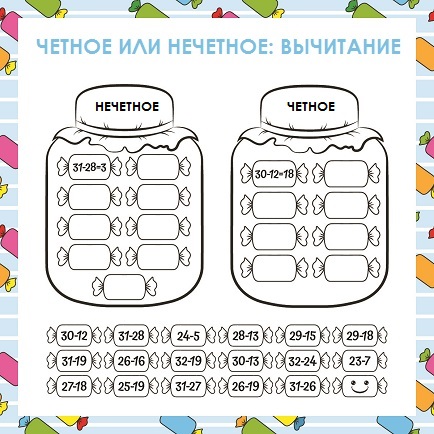
Задание 2
Вычисли значение разности и отнеси полученное число к четным или нечетным.
Популярное

15 сложных загадок на логику.

Найди закономерность

Как решать ребусы?

новые интересные статьи




