Как решать задачи на логику?

Логика – это основа рационального мышления и фундамент для развития интеллекта ребенка. Решение различных логических задач дает возможность детям научиться анализировать ситуацию, находить взаимосвязи, отличать главное и второстепенное, формировать стратегию, применять в нужном месте свои знания и навыки.

Эти умения пригодятся не только в учебе, но и в реальной жизни. Рассуждая логически, ребенок может грамотно выразить свое мнение, подойти к решению той или иной задачи более осознанно, дать обоснование всевозможным явлениям, быстро сориентироваться в ситуации.

Поэтому решение логических задач должно быть неотъемлемой частью детского развития и образования. А для того, чтобы щелкать их как орешки, нужно понимать, какими приемами и методами пользоваться при решении.

Самое главное в решении логических задач

Почти у любой задачи есть несколько вариантов решения. Чтобы легко справляться даже с самыми непростыми заданиями, надо знать, какой способ будет наиболее подходящим в той или иной ситуации.

Понимание разных методов позволяет находить оптимальный вариант решения, что особенно важно в условиях ограниченного времени.

Все задачи на развитие логики можно разделить на группы:

• Математические ребусы;
• Задачи на истинность утверждений;
• Задачи на перемещение, взвешивание или переливание;
• Задачи, которые решаются с конца;
• Работа с множествами;
• Задачи на сопоставление «Кто есть кто?»

Выбор способа решения зависит от того, к какой группе относится задание.

Известные техники решения логических задач

1. Табличный метод (таблицы соответствий, истинности, совмещенные, кубические):
   таблицы создают наглядность, прозрачность рассуждений, помогают сделать верные выводы.
2. Применение законов из алгебры логики: вводятся обозначения для простых высказываний и преобразовываются в некую формулу.
3. Метод рассуждений: подходит для решения простых задач с небольшим количеством объектов. Последовательное рассуждение над каждым условием задачи приводит к правильному выводу.
4. Черчение блок-схем: способ, подходящий для решения задач на переливание, взвешивание. Рисуется схема, на которой отмечают последовательность действий и результат, полученный при их выполнении.
5. Графический метод: подходит для решения задач на объединение или пересечение множеств. Самый популярный графический метод называется «Круги Эйлера». Нарисованная геометрическая схема наглядно показывает отношение между множествами.
6. Метод «математический бильярд»: используется для решения задач на переливание жидкостей. Вычерчивается траектория движения бильярдного шара, который отталкивается от бортов стола в форме параллелограмма.

Рассмотрим подробно самые распространенные способы, которые могут использовать в решении логических задач ученики начальных классов:

Табличный метод

Условия задачи и результаты записываем в специальную таблицу. На пересечении строк и столбцов ставим «+», если утверждения не противоречат друг другу и «-», если они расходятся.

Задача:

У Сони, Маши, Антона, Кости и Юры есть домашние животные. У каждого из ребят живет или собака, или кошка, или попугай. Вот только девочки собак не держат, а у мальчиков нет попугаев. У Сони и Маши разные питомцы, а вот у Маши с Антоном – одинаковые. У Сони нет кошки. У Кости с Юрой живут одинаковые животные, а у Антона с Костей – разные. Какие животные живут у каждого?

Решение:

Чертим таблицу, где названия столбцов – имена ребят, а названия строк – животные. Ставим в каждой ячейке знаки «+» или «-», опираясь на условия задачи:

1. Девочки собак не держат (ставим «-» на пересечении этих ячеек).
2. У мальчиков нет попугаев (в этих ячейках тоже ставим «-»).
3. У Сони нет кошки (ставим «-»).
4. Значит, у Сони есть попугай (ставим «+»).
5. У Сони и Маши разные питомцы. Получается, у Маши нет попугая (ставим «-»), зато есть кошка (ставим «+»).
6. У Маши с Антоном одинаковые животные. Значит, у Антона тоже живет кошка (ставим «+») и нет собаки (ставим «-»).
7. У Антона с Костей разные питомцы, выходит, что у Кости нет кошки (ставим «-»), зато есть собака (ставим «+»).
8. У Кости с Юрой одинаковые животные, значит у Юры тоже собака (ставим «+»), а не кошка (ставим «-»).

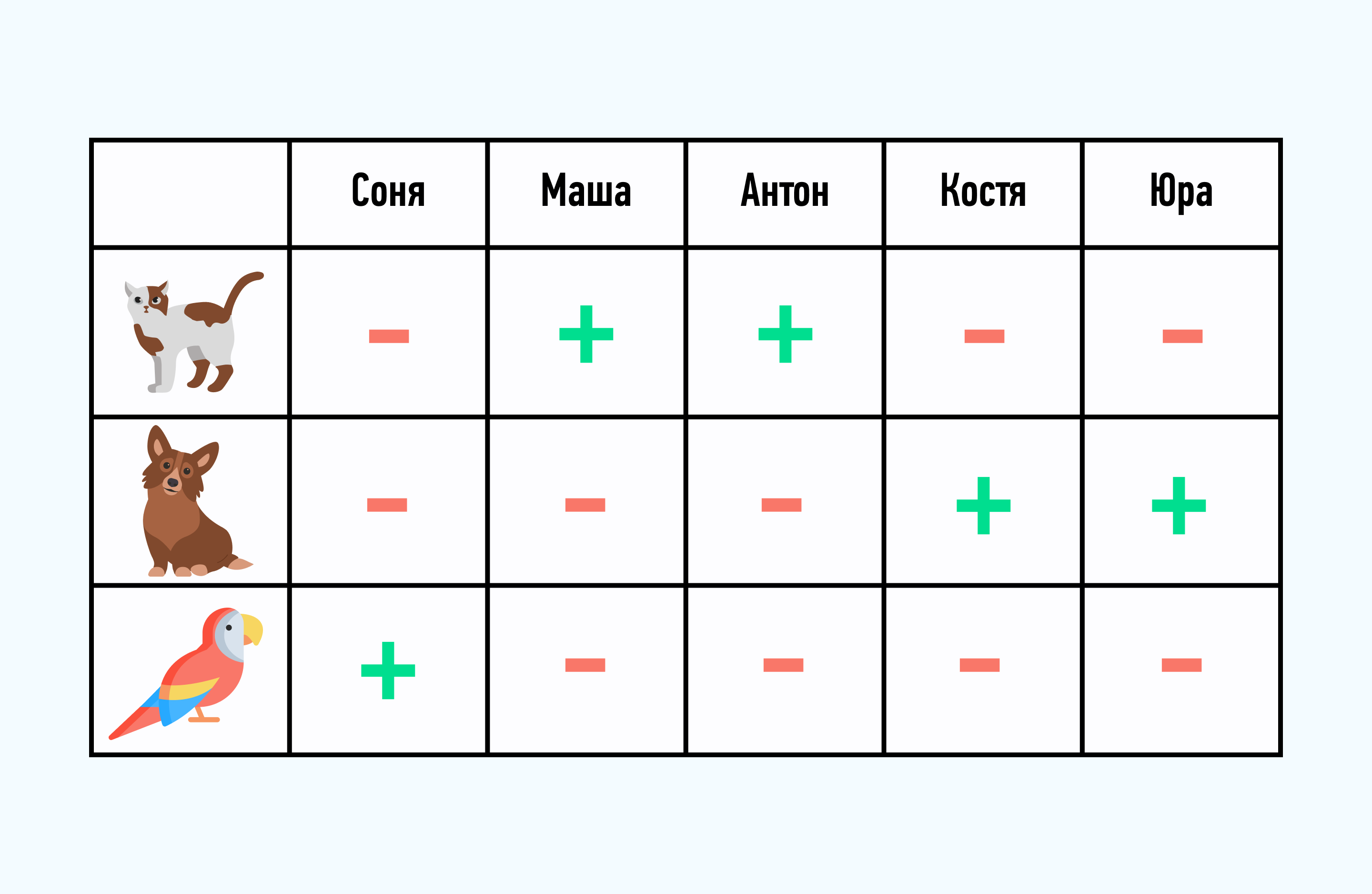
Так мы узнали, какие питомцы живут у каждого из ребят (ячейки со знаком «+»).

Ответ: У Сони попугай, у Маши и Антона кошки, у Кости и Юры собаки.

Круги Эйлера

Чтобы было легче разобраться в условиях задачи и найти решение, чертим круги, каждый из которых – отдельное множество.

Задача:

Всему классу задали на лето читать книжки. В списке литературы были такие произведения, как «Робинзон Крузо» Даниэля Дефо и «Белый клык» Джека Лондона. Известно, что 15 человек из класса прочитали «Робинзон Крузо», а остальные 11 – «Белый клык». Но среди них были 6 ребят, которые прочитали обе книги. Сколько человек прочитало только «Белый клык»?

Решение:

Чертим два круга, каждый из которых – множество детей, прочитавших определенную книгу, а пересечение кругов – дети, прочитавшие обе книги.

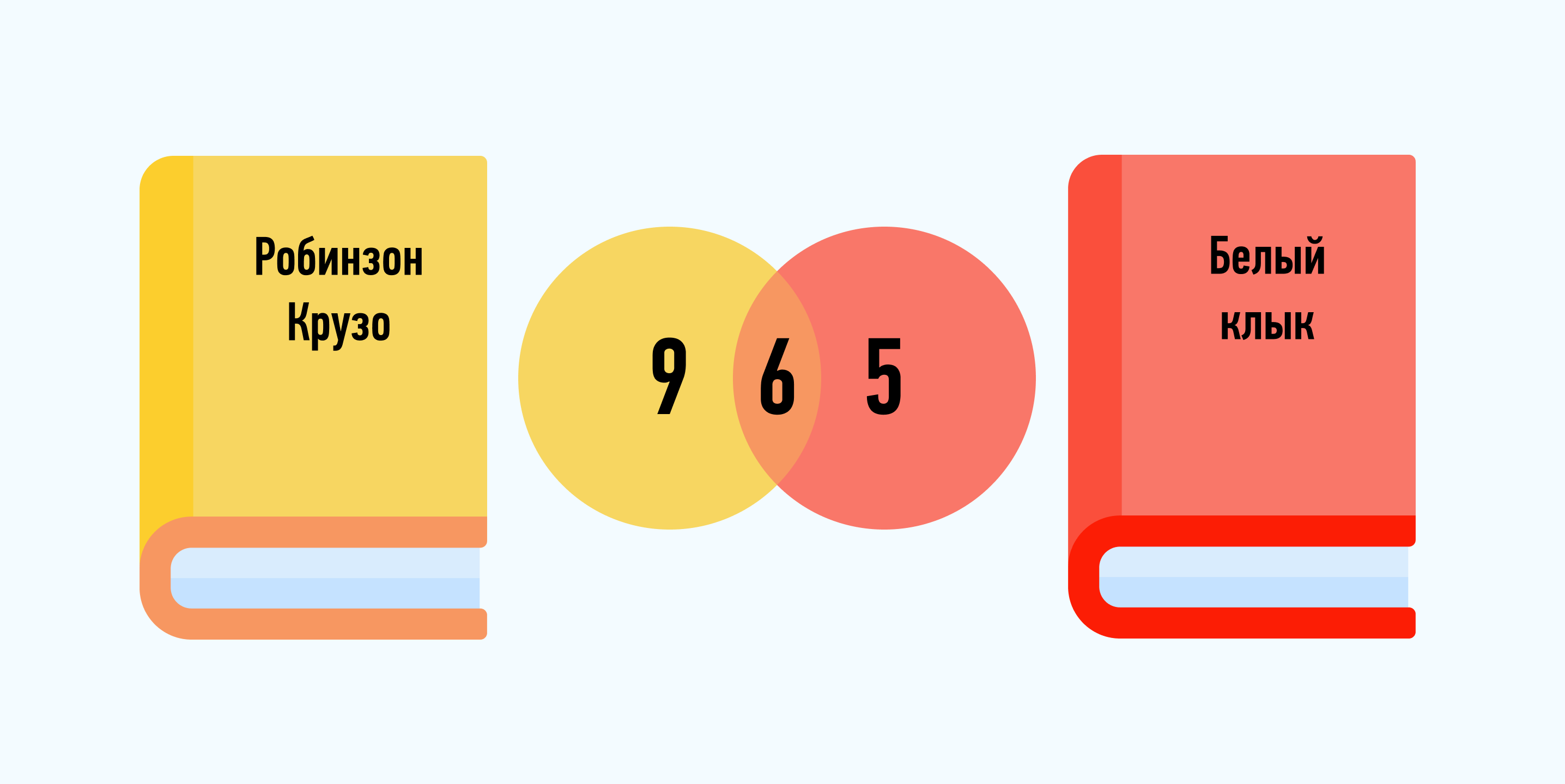
1. 15 – 6 = 9 – дети, которые прочитали только «Робинзон Крузо».
2. 11 – 6 = 5 – дети, которые читали лишь «Белый клык».

Ответ: 5 человек.

Метод рассуждений

Поочередно рассматриваем каждое из условий задачи и делаем логические выводы.

Задача:
На столе стоят вазы: голубая, зеленая, розовая и оранжевая. Третьей в ряду стоит та ваза, название цвета которой содержит больше всего букв. А зеленая стоит между оранжевой и розовой. Какая ваза стоит последней?

Решение:

1. Больше всего букв в слове «оранжевая», значит она третья по счету.
2. Если зеленая ваза стоит между оранжевой и розовой, значит, она будет второй в ряду, так как если ее поставить четвертой, то не останется места для розовой.
3. Соответственно, розовая будет стоять первой.
4. Остается голубая, она будет четвертой, то есть последней.

Ответ: голубая ваза.

Метод рассуждений «с конца»

Начинаем раскручивать клубок с конца, а затем сопоставляем результат с условиями задачи.

Задача:

Маме, папе и сыну вместе 125 лет. Когда родился сын, маме был 21 год. А папа старше мамы на 2 года. Сколько лет сейчас каждому из них?

Решение:

1. 21+2= 23 — было папе ( значит вместе родителям было 44 года)
2. (125 — 44) : 3 = 27 — возраст сына
3. 27 + 21 = 48 — возраст мамы
4. 48 + 2 = 50 — возраст папы

Ответ: 27, 48 и 50 лет.

Мы рассмотрели самые популярные и доступные методы, с помощью которых можно легко справиться с заданием. Главное – подобрать подходящий способ решения, который быстро приведет к правильному результату.

Для этого необходимо регулярно практиковаться и развивать свои способности. Отточить навыки решения подобных логических задач и многих других вы можете с помощью образовательной онлайн-платформы «Умназия».

Попробуйте решить вместе с ребенком задачу из раздела «логика» и переходите к регулярным занятиям на тренажере

Если вам понравилось, было весело интересно и полезно, то ждем вас на нашей онлайн платформе!
Умназия сегодня — это:

1. Онлайн тренажер развития навыков мышления — логики, внимания, эрудиции.
2. Программа «Культурный код» по развитию кругозора. Для самых любознательных и тех, кого кажется уже ничем не удивить!
3. Курсы развития памяти. Хотите чтобы Ваш ребенок без труда учил стихи, запоминал иностранные слова и всегда помнил про день рождения бабушки? На курсах покажем и расскажем как же этого достичь.
4. Пять ступеней финансовой грамотности. Увлекательная история героя, которая полностью зависит от действий ребенка и не имеет определенного результата. Сможет ли он пройти все финансовые ловушки и освоить пятую ступень?

Ждем вас, будет весело и интересно!

Математика и логика для детей 7-13 лет

Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате

узнать подробнее

Читайте также:

• 15 сложных загадок на логику
• Загадки на логику с подвохом
• Логические загадки для детей
• Смешные логические загадки
• Загадки Эйнштейна на логику