
Математические ребусы для детей
Ребусы — загадки, оформленные в виде картинок с буквами и знаками, — любимая детская забава. А математические ребусы — забава еще и полезная, поскольку помогает ребенку подтянуть знания по арифметике. Рассмотрим на примерах, что это за ребусы и по какому принципу они решаются.
В чем суть математических ребусов и для чего их решать?
Математические ребусы, как и привычные, представляют собой шифровку, и в них участвуют рисунки. Но, в отличие от обычных ребусов, математические требуют выполнения соответствующих операций — начиная с простых арифметических (сложение, вычитание, умножение, деление) и заканчивая построением системы уравнений. А картинками часто заменяются не слова, а цифры. Решение таких ребусов потребует не только логики и внимательности, но и умения считать.
Чтобы справиться с ребусом, нужно расставить знаки «+», «–», «:» и «*» так, чтобы получить верное равенство, или угадать числа, которые соответствуют картинке. Простейший пример: две одинаковые бабочки, между ними знак «плюс», и это равно 18 (очевидно, что за бабочками «скрывается» цифра 9).
Подобно другим ребусам и логическим задачам, математические ребусы развивают гибкость ума, усидчивость, способность мыслить и находить выход из непростых на первый взгляд ситуаций.
Благодаря регулярному разгадыванию ребусов и решению математических игр ребенку станет гораздо легче справляться со счетом, устным и письменным. В игровой форме, а тем более если в игре участвуют красочные рисунки, дети лучше и охотнее усваивают информацию. Это еще одна причина вместо очередного скучного примера предложить сыну или дочери ребус.
Какими бывают математические ребусы и как их разгадывать?
Ребус № 1
Разберем пример ребуса, для решения которого необязательно заменять рисунки цифрами, но важно уметь строить уравнения.

На чашах весов разложены фрукты и овощи. Во всех трех случаях весы находятся в равновесии, но в третьем мы не знаем, что находится на одной из чаш. От решающего требуется определить, какие фрукты и в каком количестве должны быть на последней чаше. Предлагается четыре варианта ответа.
Рассмотрим первый ребус.
В конкретном случае нам требуется в основном наблюдательность. Убрав из первого «равенства» повторяющуюся капусту, мы получим с левой стороны «уравнения» то же, что и на левой чаше весов ниже. Следовательно, мы можем приравнять то, что находится на двух правых чашах весов: груша + перец = лук + груша, то есть перец = лук. Соответственно, двум перцам соответствуют два лука. Ответ b.
Если фрукты и овощи на чашах весов не повторяются, как в данном примере, то в любом случае можно вычислить, чему равен искомый фрукт, по правилам математики, просто «уравнение» будет длиннее. Чтобы понять принцип решения более сложных «уравнений», которые без карандаша и бумаги уже не осилить, попытаемся менее очевидным путем решить это, легкое.
Итак, лимон + лук + гриб+ апельсин = груша + гриб+ перец. Поскольку в конце нам предстоит вычислить, чему соответствуют два перца, логично вычислить, чему равен один. Из первого равенства следует, что перец = лимон + лук + гриб+ апельсин – груша – гриб. По математическим законам вычеркиваем гриб со знаками «+» и «–». Получаем: перец = лимон + лук + апельсин – груша. Но из второго равенства следует, что лимон + лук + апельсин = лук + груша (лимон + апельсин = груша). Подставляем «лимон + апельсин» в первое «уравнение» вместо груши. Перец = лимон + лук + апельсин – (лимон + апельсин). Перец = лук. Следовательно, два перца = два лука (ответ b).
Второй ребус попробуйте решить самостоятельно.
- ребус 1 — b
- ребус 2 — c
Если головоломки начального уровня не вызвали у вас затруднений, смело переходите к более сложным ребусам!

- ребус 1 — 14
- ребус 2 — 18
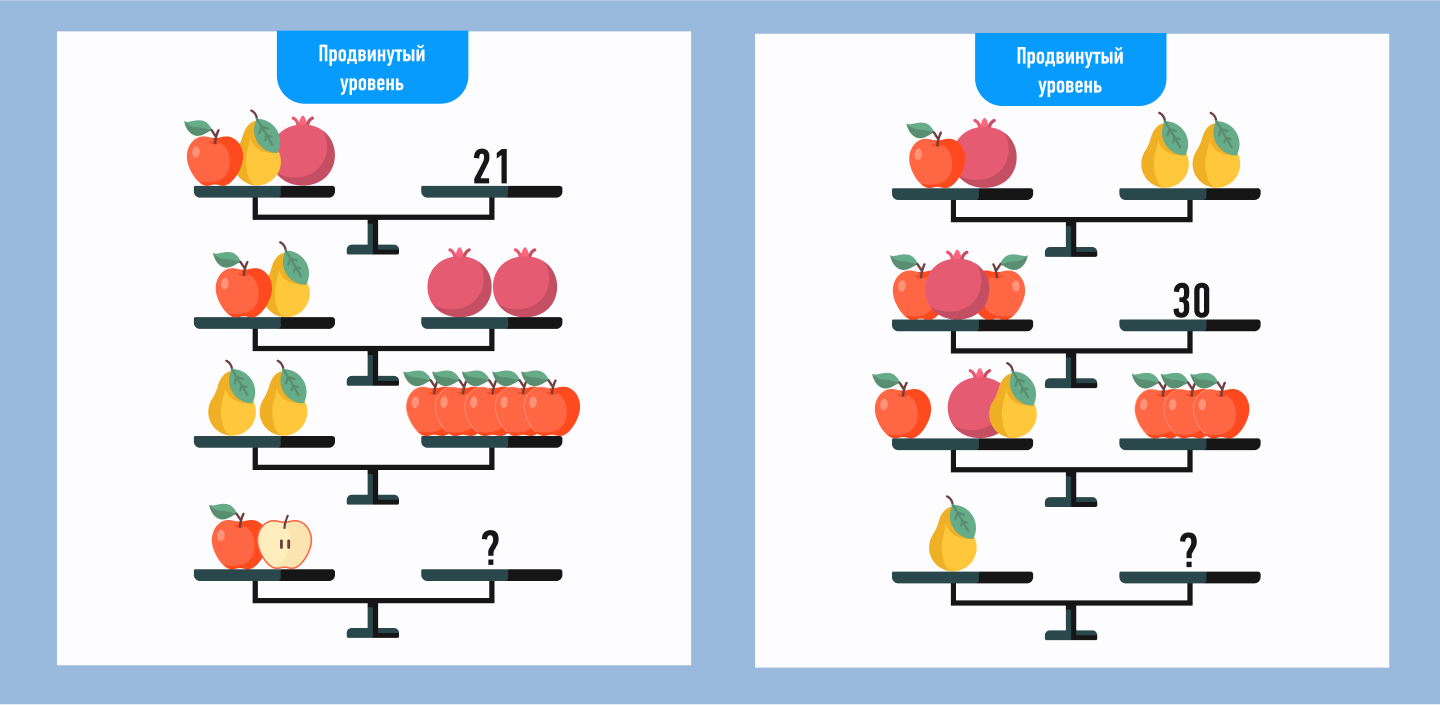
- ребус 1 — 6
- ребус 2 — 9
Ребус № 2
В другом ребусе — с бабочками — появляются уже конкретные числа. Очевидно, что каждой бабочке соответствует определенное число. Нужно определить эти числа и решить последний пример.

Рассмотрим первую «карточку».
Две голубых + две красных = 58. Две красных + две зеленых = 56. Три голубых = 39. Нам нужно решить пример «красная + голубая — зеленая + голубая».
Проще всего начать с третьего равенства — 39 : 3 = 13. Этому числу соответствует голубая бабочка.
13 * 2 + две красных = 58. Две красных = 58 — 26 = 32. Значит, одна красная = 32 : 2 = 16.
Теперь вычислим, чему равна зеленая бабочка. Для этого обратимся ко второму равенству и подставим в него уже известные нам значения: 32 + 2х = 56. 2х = 56 – 32 = 24. Так, х = 12.
Останется только подставить полученные числа в последний пример: 16 + 13 – 12 + 13 = 30.
Остальные карточки попробуйте решить самостоятельно.
- ребус 1 — 30
- ребус 2 — 37
- ребус 3 — 10
- ребус 4 — 37
- ребус 5 — 62
- ребус 6 — 24
Ребус № 3
Третий вид ребусов — с пирамидами — задачи исключительно на знание арифметики, ломать голову тут не над чем.
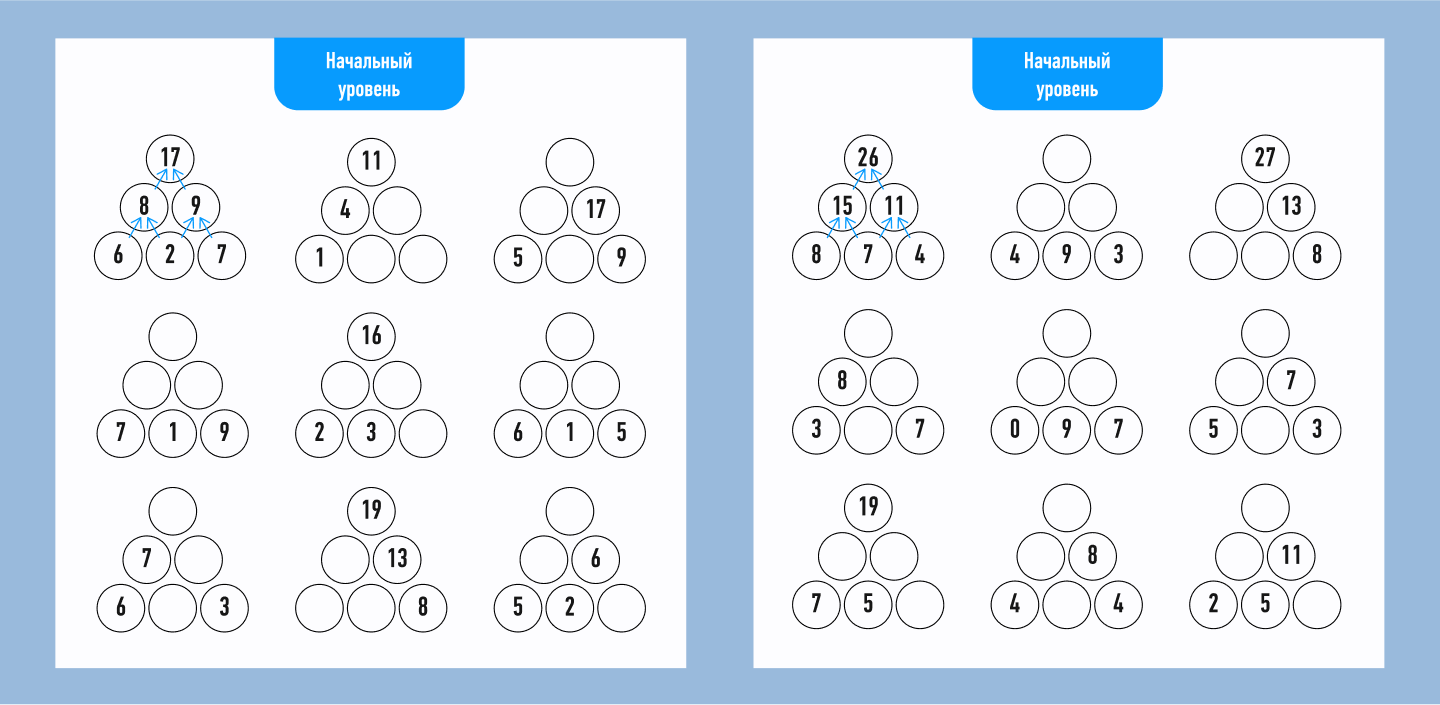
Рассмотрим, как его решать, на примере второй пирамиды с числами 1, 4 и 11.
Необходимо подставить числа в пирамиду так, чтобы два соседних в ряду образовывали в сумме число над ними.
Начнем со второго уровня пирамиды: 4 + х = 11 (число в верхнем уровне), следовательно, х = 7. На третьем, нижнем, уровне пирамиды вычислим число, которое нужно прибавить к 1, чтобы получить 4. Это 3. Таким образом, останется незаполненным всего один кружок: 7 – 3 = 4.
Предлагаем вам решить остальные пирамиды самостоятельно.
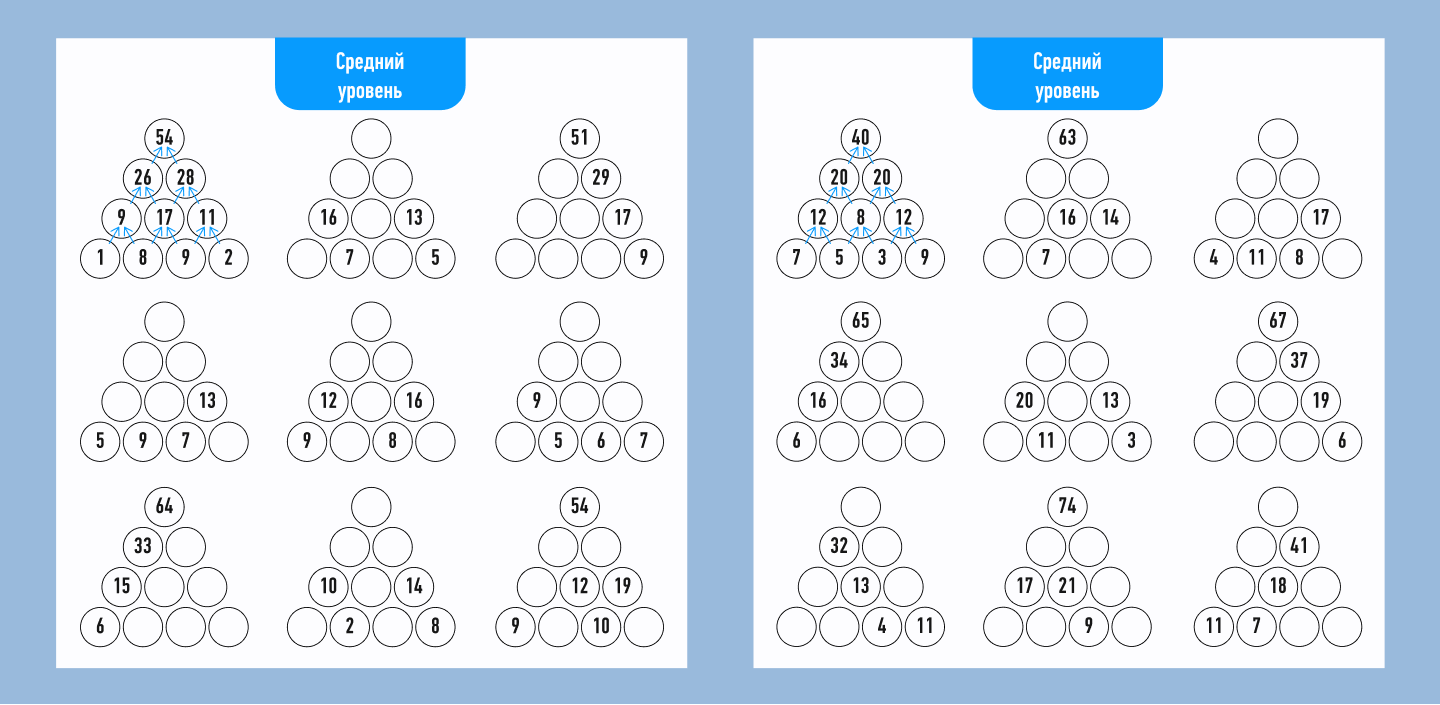
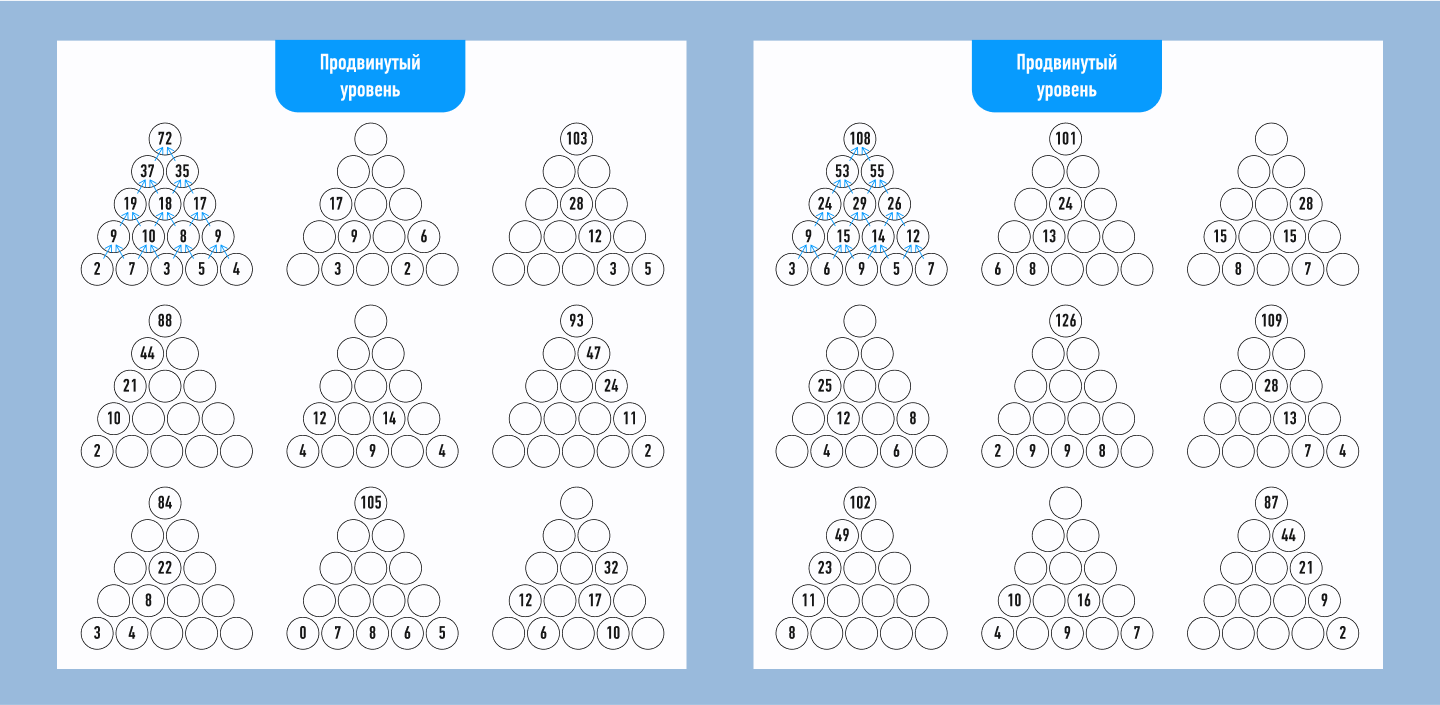
Если вы успешно справились с пирамидами для начинающих, предлагаем вам попробовать свои силы на задачках среднего и продвинутого уровня!
Ребус № 4
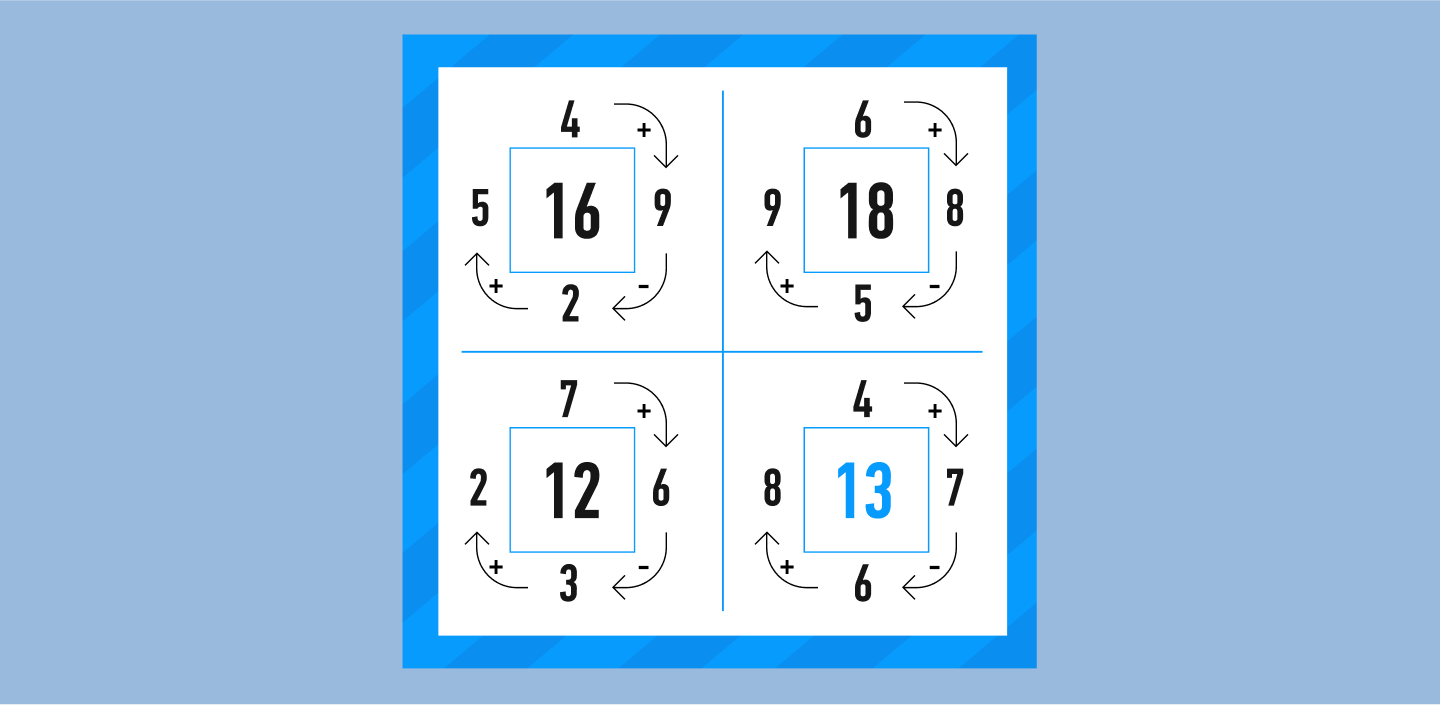
Еще один вид математических ребусов в наибольшей степени тренирует усидчивость и внимательность, поскольку единственный способ их решить — кропотливый подбор.

В первом, сравнительно простом примере нам нужно определить последовательность математических действий с предоставленными четырьмя числами, которые в результате дают число в центре. Порядок сложения/вычитания во всех примерах одинаков — уловив верную последовательность, нужно решить последний пример.
Внимательно посмотрев на числа, мы заметим, что в первых трех случаях мы получаем центральное число, используя последовательную комбинацию «+», «–», «+» и двигаясь по часовой стрелке:
- 4+ 9 – 2 + 5,
- 6 + 8 – 5 + 9,
- 7 + 6 – 3 + 2.
По той же схеме решаем наш пример: 4 + 7 – 6 + 8 = 13.
Следующие два ребуса попробуйте решить самостоятельно.


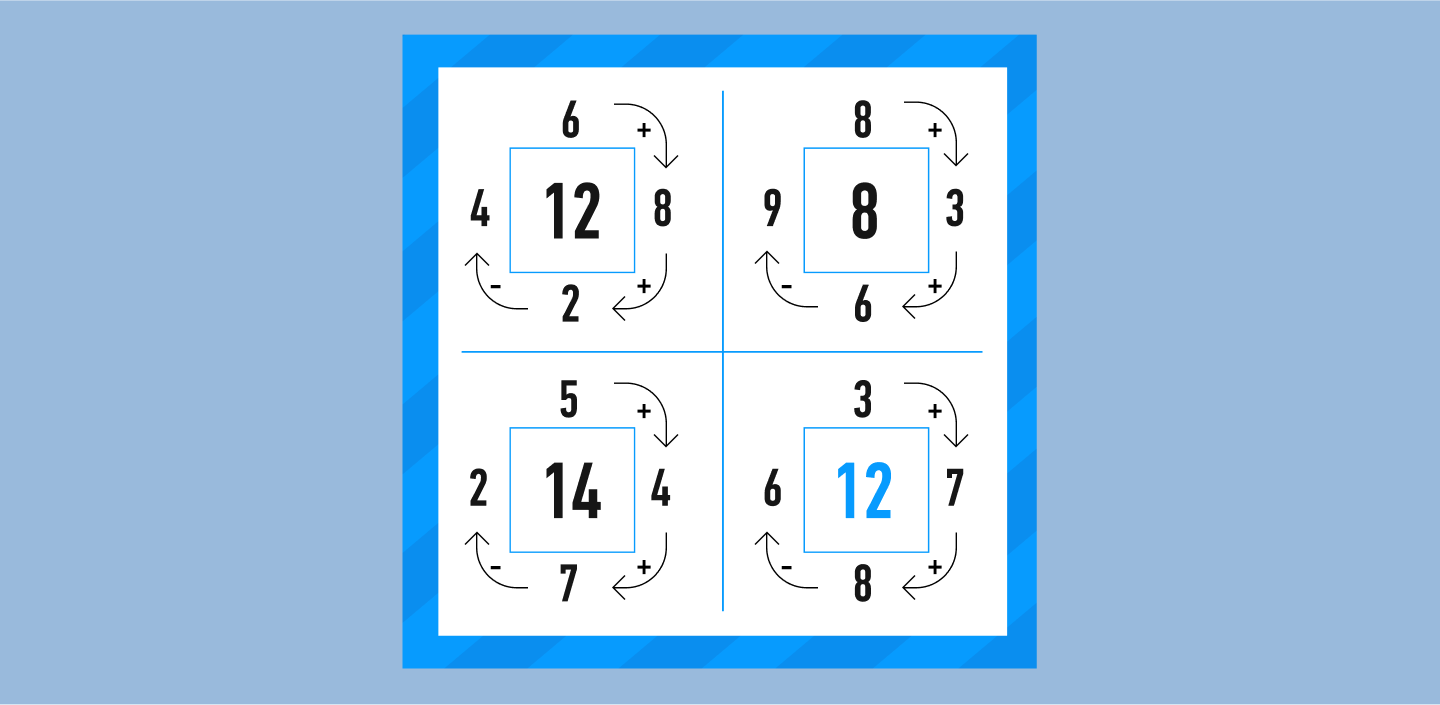
Как и любые задачи, математические ребусы бывают начального, среднего и продвинутого уровня. Зная принцип решения легких ребусов, можно перейти к более сложным и, наконец, «продвинутым».
Чем больше ребенок упражняется, тем проще ему будет «щелкать» задачи высшего уровня, а значит, тем увереннее он будет чувствовать себя на уроках математики.
Читайте также:
Математические ребусы, игры и задачи развивают умение не только оперировать числами, но и критически мыслить, рассуждать, анализировать и делать умозаключения. Умназия предлагает множество увлекательных математических задач для дошкольников и учеников начальных и средних классов. Все задания представлены в формате интерактивной игры, в процессе которой ребенок решает логические и математические задачи, помогая героям справляться с их проблемами и развивая сюжетную линию:
- задания по математике для 1 класса
- задания по математике для 2 класса
- задания по математике для 3 класса
- задания по математике для 4 класса
- задания по математике для 5 класса
Популярное

15 сложных загадок на логику.

Найди закономерность

Как решать ребусы?

новые интересные статьи




